三角恒等式的魔法六边形

 

这个六边形是个特别的图， 可以帮你记住一些 三角恒等式

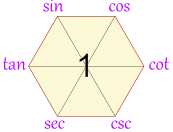若你在对三角恒等式有困难时，画这个图可能对你有帮助！

建立图形：三角恒等式

开始： tan(x) = sin(x) / cos(x) 帮你记着 想英语字母 "tsc ！"
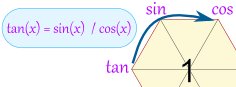加： 在六边形里 tan（正切） 的对面：cot （余切，就是 cotangent） 接下来：csc （余割，就是 cosecant)，最后 sec （正割，就是 secant）
小窍门： "co" 的函数全都在右边

 

好，画好魔法六边形了，我们怎样用他？

我们顺（或逆）时针方向移动，便可以得到所有的 "商型恒等式":

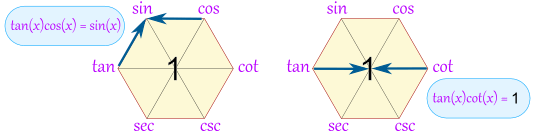
积型恒等式

六边形也显示在任何两个函数之间的函数是那两个函数的积 （若两个函数的位置是相对地区，"1" 便在它们中间）：

例子： tan(x)cos(x) = sin(x)	例子：tan(x)cot(x) = 1

更多例子：

• sin(x)csc(x) = 1
• tan(x)csc(x) = sec(x)
• sin(x)sec(x) = tan(x)

还有更多！

你也可以得到 "倒数恒等式"："通过中间的 1"

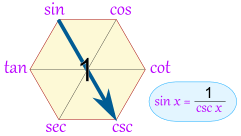你可以看到 sin(x) = 1 / csc(x)

这是全部的三角倒数恒等式：

• sin(x) = 1 / csc(x)
• cos(x) = 1 / sec(x)
• cot(x) = 1 / tan(x)
• csc(x) = 1 / sin(x)
• sec(x) = 1 / cos(x)
• tan(x) = 1 / cot(x)

额外奖励！

我们还可以得到这些：

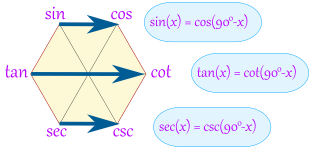
例子：

• sin(30°) = cos(60°)
• tan(80°) = cot(10°)
• sec(40°) = csc(50°)

又一个奖励：勾股恒等式

单位圆显示以下的公式：

sin² x + cos² x = 1

顺时针方向环绕魔法六边形里的三角形，可以帮我们记住这个公式：

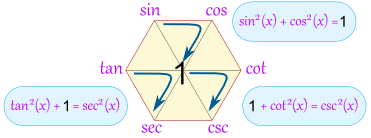
我们得到：

• sin²(x) + cos²(x) = 1
• 1 + cot²(x) = csc²(x)
• tan²(x) + 1 = sec²(x)

你也可以以逆时针方向环绕三角形，例如：

• 1 - cos²(x) = sin²(x)

希望这对你有帮助！