用导数来求极大值和极小值
函数在哪里最高或最低？微积分可以帮助你！
一个顺滑改变的函数的低点（级小值）或高点（极大值）是在其变成平坦的地方：
（但不是所有平坦的地方都是极大值或极小值，也可以有个鞍点)
在哪里变成平坦？ 在坡度等于零的地方。
坡度在哪里等于零？ 导数可以告诉我们！
（你也许想先去阅读关于 导数 的内容。）
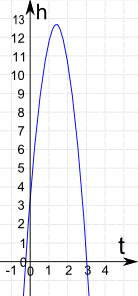
例子：向上抛一个球。在球离开手 t 秒后，它的高度是：
h = 3 + 14t − 5t2
那么球最高的高度是多少？
导数 可以给我们函数的坡度：
h = 0 + 14 − 5(2t)
= 14 − 10t
（对于这个例子你可在下面看到怎样求这个导数。）
求坡度在哪里等于零：
坡度在 t = 1.4秒 时等于零
在这个时候球的高度是：
所以：
最高的高度是 12.8 m （当 t = 1.4 s）
简略重温导数
其本上，导数 是函数的坡度。
在以上的例子中我们用：
h = 3 + 14t − 5t2
来求得这个导数：
h = 0 + 14 − 5(2t)
= 14 − 10t
它是函数在时间 t 时的坡度
有些法则可以帮助我们去求导数。
以下是一些法则：
- 常数 t（像 3）的导数是 0
- 直线，像 2x， 的导数是 2，14t 的导数是 14
- 平方函数，像 t2 的导数是 2t，所以 5t2 的导数是 5(2t) = 10t
- 和的导数是导数的和
在这里学习更多 导数法则
我们怎样知道是极大值（或极小值）？
看图就知道！如果不看图……就用导数。
取坡度的导数（原来函数的二次导数）：
14 − 10t 的导数是 −10
这个的意思是坡度持续减小（−10）：从左到右，坡度开始是正数（函数上升），经过零（平点），然后变成负数（函数下跌）：
减小（也经过 0）的坡度代表极大值。
这就是 二次导数检测
上面的图显示了前后的坡度，但在实际情况下我们在坡度为零的地方检测：
二次导数检测
若函数的 导数在 x 等于零，同时 在 x 的二次导数是：
- 小于 0，便是局部极大值
- 大于 0，便是局部极小值
- 等于 0，检测失败（但可能有其他办法）
"二次导数：小于 0 是极大值，大于 0 是极小值"
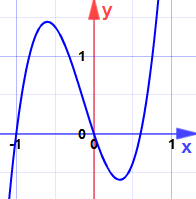
例子：求以下函数的极大值和极小值：
y = 5x3 + 2x2 − 3x
导数（坡度）是：
y = 15x2 + 4x − 3
这是个 二次式，零点在：
- x = −3/5
- x = +1/3
这两点会是极大值或极小值吗？（先别看图！）
二次导数 是 y'' = 30x + 4
在 x = −3/5：
在 x = +1/3：
（现在可以看图了。）
词汇
高点 叫 极大值。
低点 叫 极小值。
两者 都叫 极值。
若函数可能在别的地方有更高（或更低）的值，但在这点附近没有，我们便叫这点为 局部极大值（或极小值）。
再举个例
例子：求以下的极大值和极小值：
y = x3 − 6x2 + 12x − 5
导数：
y = 3x2 − 12x + 12
是个 二次式，只在 x = 2 有个零点
是个极大值还是极小值？
二次导数 是 y'' = 6x − 12
在 x = 2：
原因是：
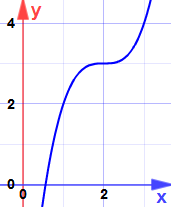
这是个 鞍点 …… 坡度变成零，但不是极大值，也不是极小值。
一定要是可微分的。
有一个重要的技术点：
函数一定要是 可微分的 （导数存在于在函数定义域里的每个点）。
（函数也一定要是 连续的，但任何可微分的函数都是连续的。）