分离变量法

分离变量法是是一个特别的解微分方程方法

微分方程是有函数及其一个或以上的导数的方程：

dy/dx = 5xy
例子：有函数 y 和其导数的方程 dy dx

什么时候可以用？

分离变量法：dy/dx = 5xy 变成 dy/y = 5x dx

在以下的情形可以应用分离变量法：

所有 y 项（包括 dy）可以被移到方程的一边，

所有 x 项（包括 dx）可以被移到另一边。

方法

方法有三步：

一、把所有 y 项（包括 dy）移到方程的一边，把所有 x 项（包括 dx）移到另一边。
二、把一边对 y 积分，另一边对 x 积分。不要忘了 "+ C" （积分常数）。
三、简化

例子：解（k 是常数）

dy dx = ky

一、分离变量：把所有 y 项移到方程的一边，把所有 x 项移到方程的另一边。

每边乘以 dx：		dy = ky dx
每边除以 y：		dy y = k dx

二、每边分开来求积分：

积分符号放在前面：		∫ dy y = ∫k dx
求左边的积分：		ln(y) + C = ∫k dx
求右边的积分：		ln(y) + C = kx + D

C 是积分常数。用 D 来代表另一个（不同的）积分常数。

三、简化

合并两个常数为一个(a=D−C):		ln(y) = kx + a
e^(ln(y)) = y，所以我们取每边的幂：		y = e^{kx + a}
e^{kx + a} = e^kx e^a，所以这是：		y = e^kx e^a
e^a 是个常数，我们用 c 来代替它		y = ce^kx

解了：

y = ce^kx

这是个一般的一阶微分方程，在很多不同的实际情况下都会出现。

在上面我们用了 y 和 x，用其他的名字来代表变量也是可以的：

例子：兔子！

有越多兔子就会越多小兔子，小兔子长大后又会生小兔子。这样，兔子的数量会增长得越来越快！

重要的信息是：

在任何时间 t 时兔子的数量 N
增长率 r
数量变化率 dN dt

在任何时间的变化率是增长率乘以在那一刻的数量：

dN dt = rN

慢着！这和上面例子是同一个方程，只不过字母不同：

是 N，不是 y
是 t，不是 x
是 r，不是 k

所以解是（同上）：

N = ce^rt

举个例子，这是 N = 0.3e^2t 的图：

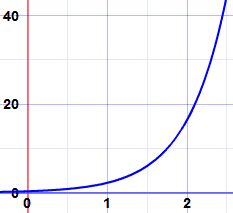
指数式增长

还有其他类似的方程，例如连续复利。

更多例子

我们现在再来看一些分离变量法的例子：

例子：解

dy	=	1
dx	=	y

一、分离变量：把所有 y 项移到方程的一边，把所有 x 项移到方程的另一边。

每边乘以 dx： dy = (1/y) dx

每边乘以 y： y dy = dx

二、每边分开来求积分：

放积分符号在前面： ∫y dy = ∫dx

每边求积分： (y²)/2 = x + C

我们在同一行求两边的积分。

我们还用了一个捷径：只用一个积分常数 C。这没什么不妥，因为我们可以用 +D 和 +E，然后设 C = E−D。

三、简化 y

每边乘以 2： y² = 2(x + C)

每边取平方根： y = ±√(2(x + C))

注意：这和 y = √(2x) + C 不同，因为 C 是在取平方根之前加的。在解微分方程时常会遇到这种情形，我们不能在最后才加 C，一定要在求积分时加上去。

解了：

y = ±√(2(x + C))

比较复杂的例子：

例子：解

dy = 2xy

dx 1 + x²

一、分离变量

每边乘以 dx，每边除以 y：

1 dy = 2x dx

y 1 + x²

二、每边分开来求积分：

积分符号放在前面：

∫ 1 dy = ∫ 2x dx

y 1 + x²

左边是个简单的对数，右边可以用换元积分法来做：

设 u = 1 + x²，所以 du = 2x dx

∫ 1 dy = ∫ 1 du

y u

求积分： ln(y) = ln(u) + C

设 C = ln(k)： ln(y) = ln(u) + ln(k)

来得到这个： y = uk

再代回 u = 1 + x²： y = k(1 + x²)

三、简化

不能再简化，我们求到解了：

y = k(1 + x²)

更困难的例子：著名的费尔哈斯公式

例子：又是兔子！

上面的增长微分方程是：

dN = rN

dt

增长不能无穷延续下去，食物早晚都会被吃光。

数学家费尔哈斯把食物可以维持最大的兔子数量 k 也算在方程里，他的结果是：

dN = rN(1-N/k)

dt

费尔哈斯公式

这个可以解吗？

可以，但是要用一个技巧 ……

一、分离变量

每边乘以 dt: dN = rN(1−N/k) dt

每边除以 N(1-N/k):

1 dN = r dt

N(1−N/k)

二、求积分

放积分符号在前面：

∫ 1 dN = ∫r dt

N(1−N/k)

嗯 …… 左边好像很难积分。其实用一个技巧便可以做到。

这样开始：

1

N(1−N/k)

上面和下面都乘以 k:

k

N(k−N)

现在用这个技巧：在上面加 N 和 −N
（去看看部分分式）：

N+k−N

N(k−N)

拆开为两个分数：

N + k−N

N(k−N) N(k−N)

简化每个分数：

1 + 1

k−N N

现在可以分开来求积分来了：

∫ 1 dN + ∫ 1 dN = ∫r dt

k−N N

求积分： −ln(k−N) + ln(N) = rt + C

大功告成！

（为什么变成负 ln(k−N）？因为我们是对 N 求积分。）

三、简化

取所有项的负值： ln(k−N) − ln(N) = −rt − C

合并 ln()： ln((k−N)/N) = −rt − C

取每边的幂： (k−N)/N = e^−rt−C

分离 e 的幂： (k−N)/N = e^−rt e^−C

e^−C 是常数，我们可以用 A 来代替它： (k−N)/N = Ae^−rt

差不多了！用一点代数来把 N 分解出来：

分离分数项： (k/N)−1 = Ae^−rt

每边加 1： k/N = 1 + Ae^−rt

除以 k： 1/N = (1 + Ae^−rt)/k

每边取倒数： N = k/(1 + Ae^−rt)

解了：

N = k

1 + Ae^−rt

举个例，这是 40 的图：

1 + 5e^−2t

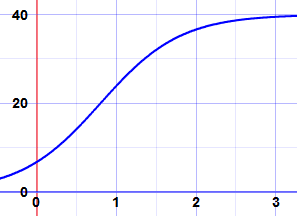
开始时，函数指数式增加，
到 k=40 时变得平坦了

微分方程微积分索引

放积分符号在前面：		∫y dy = ∫dx
每边求积分：		(y²)/2 = x + C

每边乘以 2：		y² = 2(x + C)
每边取平方根：		y = ±√(2(x + C))

取所有项的负值：		ln(k−N) − ln(N) = −rt − C
合并 ln()：		ln((k−N)/N) = −rt − C
取每边的幂：		(k−N)/N = e^−rt−C
分离 e 的幂：		(k−N)/N = e^−rt e^−C
e^−C 是常数，我们可以用 A 来代替它：		(k−N)/N = Ae^−rt

分离分数项：		(k/N)−1 = Ae^−rt
每边加 1：		k/N = 1 + Ae^−rt
除以 k：		1/N = (1 + Ae^−rt)/k
每边取倒数：		N = k/(1 + Ae^−rt)