弧度
把半径放到圆周上
所形成的角度:
|
1弧度是 大约 57.2958角度。 |
为什么是 "57.2958……" 度?下面我们会解释。
弧度是基于圆的半径的纯计量单位:
弧度:把半径放到圆周上
所形成的角度。
弧度与角度
我们现在来看看为什么 1弧度等于 57.2958……角度:
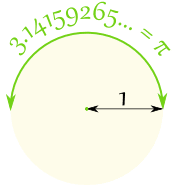
在一个半圆上有 π 弧度,也等于 180°
| 所以: | π 弧度 | = | 180° | |
| 那么: | 1弧度 | = | 180°/π | |
| = | 57.2958……° | |||
| (大约) |
将弧度转换为角度:乘以 180,除以 π
将角度转换为弧度:乘以 π,除以 180
这是弧度与角度的对照列表:
| 角度 | 弧度 (精确) |
弧度 (近似) |
|---|---|---|
| 30° | π/6 | 0.524 |
| 45° | π/4 | 0.785 |
| 60° | π/3 | 1.047 |
| 90° | π/2 | 1.571 |
| 180° | π | 3.142 |
| 270° | 3π/2 | 4.712 |
| 360° | 2π | 6.283 |
数学家喜欢用弧度
因为弧度是基于 "半径环绕圆周" 的概念,在数学里用弧度来做计算会得到自然并且简单的答案。
例如,看看变量很小时的正弦函数:
| x (radians) | 1 | 0.1 | 0.01 | 0.001 |
|---|---|---|---|---|
| sin(x) | 0.8414710 | 0.0998334 | 0.0099998 | 0.0009999998 |
当变量(x)是非常小的时候,"x" 和 "sin(x)" 的值是差不多相等的
(但 "x" 一定要是弧度!)
(但 "x" 一定要是弧度!)
在数学里有很多类似的例子。
结论
所以在日常生活中,角度比较容易使用,但在数学中,弧度就比较合适。